Storing Hierarchical Data in a Database

Storing hierarchical data in a database: two approaches for stable storage and fast reporting of tree data.

Many times we need to store enormous amounts of —tree— or —hierarchical— data:

• Hundreds of categories, sub-categories and sub-sub-categories in a single online store
• Navigation menus of extremely complex sitemaps
• Relationship of members who are involved in affiliate marketing campaigns

Proper organization and indexing of this data will make it possible to easily:

• Display results (how do you build a navigation tree?)
• Report on statistics (how many people are in this member's affiliate down-line?)
• Extract a specific segment of the tree desired (do you want to show the sub-nav in the side bar of a category detail page?)

Adjacent List Model: the —parent-child— method

The standard method of storing hierarchical data is simple parent-child relationship. Each record in the database includes a —parent id—, and a recursive query through the records build the children, siblings, and levels of the tree. Adding a new record to the system only requires the ID of the parent, with no other indexing. The advantages of this method are the simplicity, and low-cost of entering new records. If you add a child record, you simply need to know the parent ID and everything else will build out fine. The cost comes to building out the tree, or running reports on the data when you get into larger data sets. This might not be any big deal for a small navigation tree, but if you are trying to show the genealogy of an affiliate marketing team the numbers can get into the thousands, and the recursion through the data can be brutal.

Parent Child Tree

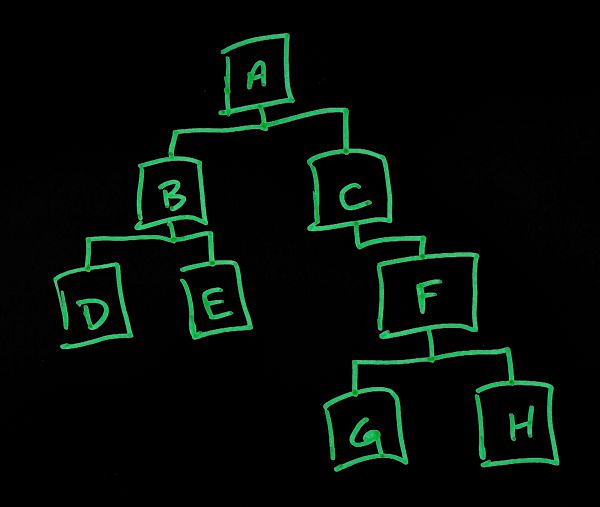
Parent - Child Relationship, the storage of the Parent ID

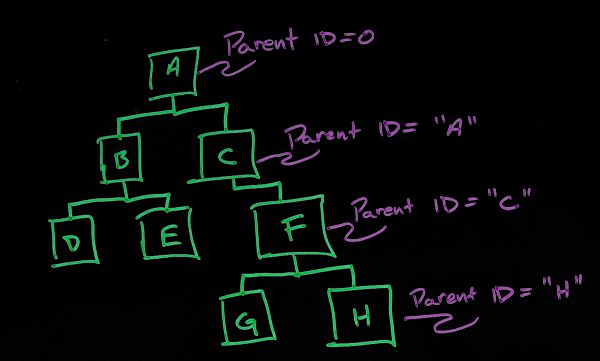
Pros:

• Easy to insert new data (no indexing required)
• Lightweight storage of data (only one field —parent id— required to build an entire affiliate tree)
• —levels of the tree— (how deep you are) is inherently obvious, as each level requires a new query.

Cons:

• Very intensive overhead to report

Example: "Show all child records of a single node"

Given parent "A", build a tree of all members of the affiliate downline:

• First show all records with Parent ID = "A"
• For each of these records, find the records that have the corresponding parent ID
• Rinse and repeat. (one query per level, but if you want to get the granularity, you may have to run one query per each child record)
  
  

You can see how quickly the queries add up, and come at a heavy cost.

Nested Sets to the rescue!

Another technique is to build an index for each record using nested sets. In a nested set, each record contains two indices, a "left" and "right" index number. The indexes are created by starting at the root of the tree, and working from left to right through each node of the tree.

In standard tree-format, this looks confusing and difficult to manage.

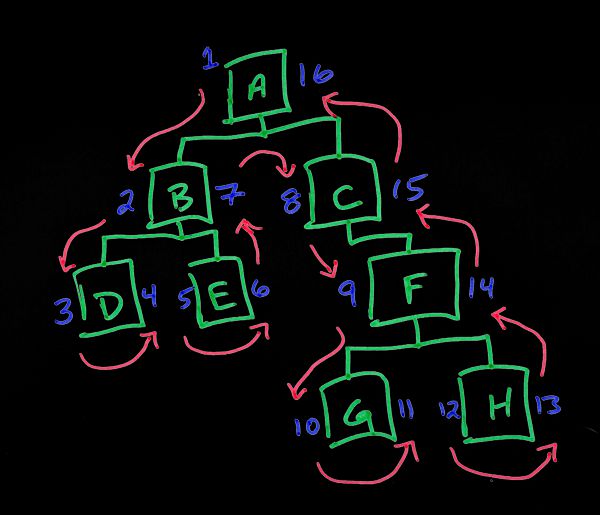
But, view the data set from the TOP and the brilliance shines through. Each node, in essence, is a container holding the indexes of each of the child nodes below. The left and right index numbers now line up from left to right. If there are any child records, the left and right indexes of the children will be a number larger then the left of the parent, and smaller than the right.

Here's an example:

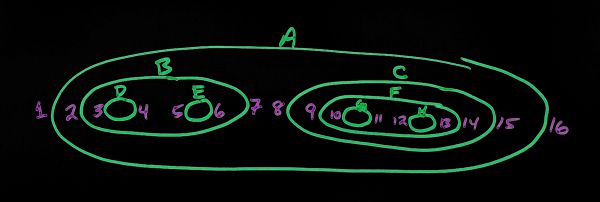
Pros

• Reporting is easy and lightweight
• Quick selection of downline sets

Cons

• Adding or removing records requires a re-index of the entire tree
• Report details (such as finding the number of levels in the child-set of records) can require complex queries

Example: "how many children are below node A"?

Because of the pre-indexing of the nodes, you only need to take the difference between the left and right nodes, subtract 1 and divide by 2 to get the total number of children of a given node. This can be done without any queries involving the children themselves.

Node A

Index "left" = 1

Index "right" = 16

((Right - Left) - 1) / 2 = Total Number of Children

((16 - 1) - 1)/2 = 8 nodes